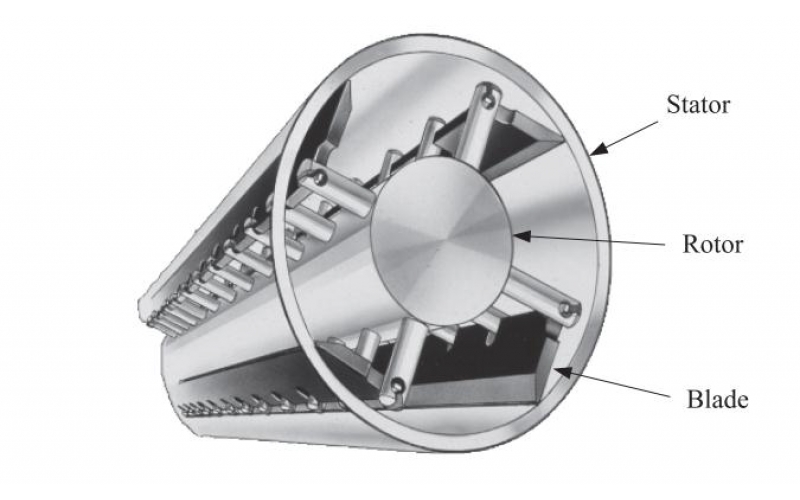
Tiek parādīts vienkāršs matemātiskais šķidruma plūsmas modelis izplatītā tipa nokasītās virsmas siltummainī, kurā spraugas starp lāpstiņām un ierīces sienām ir šauras, lai būtu derīgs plūsmas eļļošanas teorijas apraksts.Konkrēti, tiek analizēta vienmērīga Ņūtona šķidruma izotermiskā plūsma ap periodisku šarnīra skrāpju lāpstiņu masīvu kanālā ar vienu nekustīgu un vienu kustīgu sienu, kad tiek pielietots spiediena gradients virzienā, kas ir perpendikulārs sienas kustībai.Plūsma ir trīsdimensiju, bet dabiski sadalās divdimensiju “šķērsvirziena” plūsmā, ko virza robežkustība, un “gareniskā” spiediena vadītā plūsmā.Vispirms tiek iegūtas detaļas par šķērseniskās plūsmas struktūru, un jo īpaši tiek aprēķinātas lāpstiņu līdzsvara pozīcijas.Tiek parādīts, ka tiks sasniegts vēlamais kontakts starp asmeņiem un kustīgo sienu, ja asmeņi ir pagriezti pietiekami tuvu to galiem.Kad tiek sasniegts vēlamais kontakts, modelis paredz, ka spēki un griezes momenti uz asmeņiem ir vienskaitlī, un tāpēc modelis tiek vispārināts, iekļaujot trīs papildu fiziskus efektus, proti, neņūtona spēka likuma uzvedību, slīdēšanu pie stingrām robežām un kavitāciju. reģionos ar ļoti zemu spiedienu, un katrs no tiem atrisina šīs singularitātes.Visbeidzot, tiek apspriests gareniskās plūsmas raksturs.
Publicēšanas laiks: 22. jūnijs 2021